Aproximaciones y errores

Definición de errores

Estos errores surgen al momento de realizar aproximaciones al representar operaciones y cantidades matemáticas debido a la imposibilidad de controlar la influencia de todas las variables.

Error absoluto (Ea): el error absoluto es la es la diferencia del valor de la aproximado (medida) y el valor tomado como exacto, el resultado puede ser negativo o positivo, según se la medida es superior al valor real o inferior (la resta sale positiva o negativa) al cual se le sacara el valor absoluto. El resultado tendrá las mismas unidades del valor exacto o aproximado.

Sea p un valor exacto o verdadero y p1 el valor aproximado

Error relativo (Er): El error relativo resulta de la división entre el error absoluto y el valor exacto. Este error no tiene unidades.

Cifras significativas

Son significativos todos los dígitos distintos de cero.

8723 y 0.04578 tienen cuatro cifras significativas

Los ceros situados entre dos cifras significativas son significativos.

105 y 0.0205 tienen tres cifras significativas

Los ceros a la izquierda de la primera cifra significativa no lo son.

0,005 y 0.06 tienen una cifra significativa
ORDEN DE DESCOMPOSICIÓN POLINÓMICA
El orden de una descomposición polinomica viene a ser el exponente máximo de una descomposición polinomica

CIFRAS SIGNIFICATIVAS EXACTAS
Esta esta definida por la relación:
CIFRAS DECIMALES EXACTAS

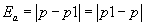
Comentarios

Entradas populares de este blog

Método de regula falsi (regla falsa) o falsa posición

Método de regula falsi (regla falsa) o falsa posición es un método iterativo que a diferencia del método de la bisección, este se basa en una visualización grafica que consiste en unir f(a 0 ) y f(b 0 ) con una línea recta, la intersección de esta recta con el eje de coordenadas x representa una mejor aproximación de la raíz que por el método de la bisección, aunque no siempre es así. Hallaremos la pendiente de la grafica de la recta trazada entre los puntos (a,f(a)) y (b,f(b)), donde la intersección con el eje de abscisas o línea horizontal sera nuestra aproximación a la raíz x i . Podremos notar que la regula falsi determina el promedio ponderado de los extremos del intervalo. Algoritmo de la falsa posición Paso 1: dada la ecuación f(x)=0 ubicar el intervalo donde exista la raíz r є [a , b] Paso 2: generar la sucesión {x i } con la siguiente relación. Paso 3: Determinar Paso 4: si |x-...

TEOREMA DE BOLZANO

Se la ecuación f(x)=0 , donde f(x) es una función polinómica o trascendente y además está definida en el intervalo [a,b]. Partiremos del intervalo [a.b] iremos tabulando en cada intervalo de longitud 1 para ver en que intervalos encontramos raíces bajo la siguiente condición . Ejemplo Localizaremos el intervalo donde se encuentra la raíz de la ecuación: Ahora tabularemos la función f(x) para un intervalo de x esta dentro de [-1,10] y obtenemos la gráfica. Observamos que hay raices en los intervalos [0,1], [3,4], [6,7] y [9,10]

MÉTODO DE BISECCIÓN

El método de bisección sirve resolver ecuaciones en una variable. Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f ( a ) y f ( b ) si f ( a ) x f ( b )<0 entonces existe un numero llamado raiz “r” tal que f(r)=0. De esta forma, se asegura la existencia de al menos una solución o raíz de la ecuación f (x)=0. Luego el intervalo se divide en dos, si la función cambia de signo en uno de los nuevos intervalos, este se vuelve a dividir y así sucesivamente hasta obtener una aproximación adecuada. Algoritmo de bisección Paso 1: Usando el teorema de Bolzano localizar los intervalos en los que podemos encontrar al menos una raíz f ( a ) x f ( b )<0 y localizamos el valor inferior a i y el valor superior b i del intervalo que encierra la raíz Paso 2: Realizar una aproximac...

MÉTODOS NUMÉRICOS

Buscar este blog